Формула площади правильного треугольника, Площадь правильного треугольника. Площадь квадрата. Площадь правильного шестиугольника

Материал из Википедии — свободной энциклопедии. Только в правильном треугольнике возможно нахождение площади полной поверхности через сторону. Свойства логарифмов.
Все способы будут рассмотрены в этой статье. Это свойство характерно для равнобедренных треугольников, но любой правильный треугольник и будет равнобедренным, просто любая из его сторон может считаться основанием, так как две другие стороны в любом случае будут равны.
В результате треугольник делиться на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для правильного треугольника.
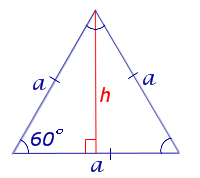
Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет АМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса. Значит можно выразить значение АМ:. В заданном треугольнике это будет выглядеть следующим образом:. ВС заменили на а, так как все стороны равны между собой, а значение высоты мы находили ранее.
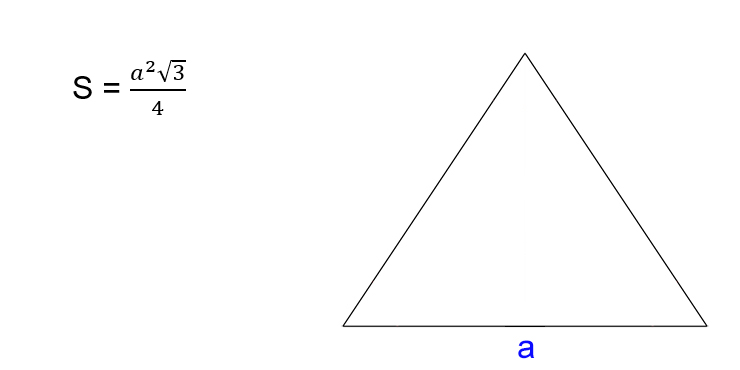
Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике. Только в правильном треугольнике возможно нахождение площади полной поверхности через сторону.
По той же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника.
Прежде чем использовать эту формулу необходимо доказать, что треугольник правильный или убедиться, что это условие прописано в исходных данных задачи. Основные свойства площадей треугольников. Теорема синусов. Теорема косинусов. Центральные углы. Вписанные углы. Угол между хордами. Угол между секущими. Угол между касательной и хордой.
Свойства касательных, секущих и хорд окружности. Радикальная ось. Вписанная окружность описанный треугольник, описанный четырехугольник. Описанная окружность вписанный треугольник, вписанный четырехугольник. Теорема Вариньона.
Теорема Менелая. Теорема Чевы. Теорема Ван-Обеля. Теорема Стюарта. Длина биссектрисы и длина медианы треугольника. Площадь выпуклого четырехугольника. Площадь треугольника. Формула Герона. Площадь параллелограмма. Площадь ромба. Площадь прямоугольника.
Площадь квадрата. Площадь трапеции. Площадь правильного треугольника. Площадь правильного шестиугольника. Длина окружности.
Длина дуги. Площадь круга. Площадь сектора. Длина отрезка. Середина отрезка. Координаты вектора. Сложение векторов. Скалярное произведение векторов. Формулы Справочник с основными фактами стереометрии.
Теорема о трех перпендикулярах. Прямая призма. Правильная призма. Объем призмы. Прямоугольный параллелепипед.
Объем параллелепипеда. Объем куба. Диагональ куба. Площадь поверхности куба. Прямоугольная пирамида. Правильная пирамида. Объем пирамиды. Объем цилиндра. Площадь поверхности цилиндра.

Объем конуса. Площадь поверхности конуса. Объем шара. Площадь поверхности сферы. Шаровой слой. Шаровой сектор. Шаровой сегмент. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми. Геометрия на плоскости планиметрия. Часть I. Подробная теория Введение в планиметрию. Основные факты о треугольниках. Выпуклый четырехугольник. Прямоугольник и квадрат. Площади многоугольников.
Подобие треугольников.
Средняя линия треугольника. Важные факты о высоте, биссектрисе и медиане. Длина дуги окружности. Площадь кругового сектора. Часть II. Подробная теория Начальные сведения о синусе, косинусе, тангенсе и котангенсе.
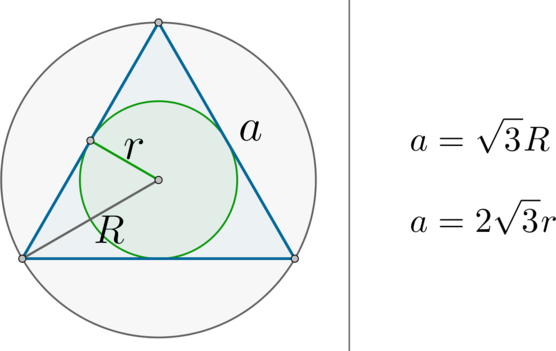
Основные теоремы. Окружность: описанная около многоугольника. Окружность: вписанная в многоугольник или угол. Теорема синусов и теорема косинусов. Правильный шестиугольник и его свойства. Начальные сведения. Векторы на координатной плоскости. Часть III. Важные теоремы для решения задания 16 Метод площадей для решения задач. Основные теоремы, связанные с окружностями.
Подобие треугольников и пропорциональные отрезки. Задачи на теоремы Менелая, Чевы и Стюарта. Формулы для биссектрисы и медианы. Геометрия в пространстве стереометрия. Подробная теория Введение в стереометрию. Углы и расстояния в пространстве. Поверхности вращения: цилиндр, конус, сфера. Построение сечений. Подробная теория: рациональные и десятичные дроби, квадратные корни Рациональные обыкновенные дроби и действия с ними.
Простые числа. Десятичные дроби и действия с ними. Квадратный корень. Действия с квадратными корнями. Сравнение квадратных корней. Простейшие уравнения.
Задание 5 Линейные, квадратные и простейшие кубические уравнения. Простейшие рациональные уравнения. Простейшие иррациональные уравнения.
Простейшие показательные уравнения с неизвестной в показателе степени. Простейшие логарифмические уравнения. Задания 5 и 13 Введение в тригонометрию. Простейшие тригонометрические уравнения задание 5 и неравенства. Решение простейших тригонометрических уравнений с помощью аркфункций.
Их вывод. Основные виды тригонометрических уравнений задание